Semi-analytical hydrodynamics with MEEM
- rebecca-mc

- Dec 7, 2025
- 7 min read
(This is my first post in a while, and I decided to make it more blog style instead of portfolio style. Hope you enjoy it).
MEEM, or the matched eigenfunction expansion method, is a semi-analytical method for solving a PDE boundary value problem. It was developed in 1980 by Prof. Ronald Yeung to find the wave radiation forces on a truncated cylinder, and has since been expanded to other geometries.

The method applies to geometries that are too complex to have a fully analytical solution but simple enough such that the analytical solution can be applied separately in discrete zones of the problem, and then adjacent zones numerically matched for consistency (hence the term semi-analytical).
I first learned about this method in fall 2022 and I worked with another PhD student in my lab to implement it for the final project of our hydrodynamics class, MAE 6350. While the math was settled decades ago, the method had received surprisingly little attention from ocean engineers and other practitioners, and its use was isolated to a few hydrodynamics research labs around the world (one of which being Prof. Yeung's). There were not any open-source or even closed-source commercial implementations that we could find, even after reaching out to authors of the relevant papers, so we set out to code it up ourselves.
The math was pretty complicated, but Prof. Yeung had already worked it all out 40+ years ago, so how hard could it be?

The implementation seemed deceptively simple, and we had a running version in MATLAB within a week or two: implementing functions for each of the eigenfunctions and potential expressions, assembling into a matrix, solving the matrix equations for the unknown eigen-coefficients, and substituting the coefficients back in to the potential expression to evaluate the fluid velocity field.
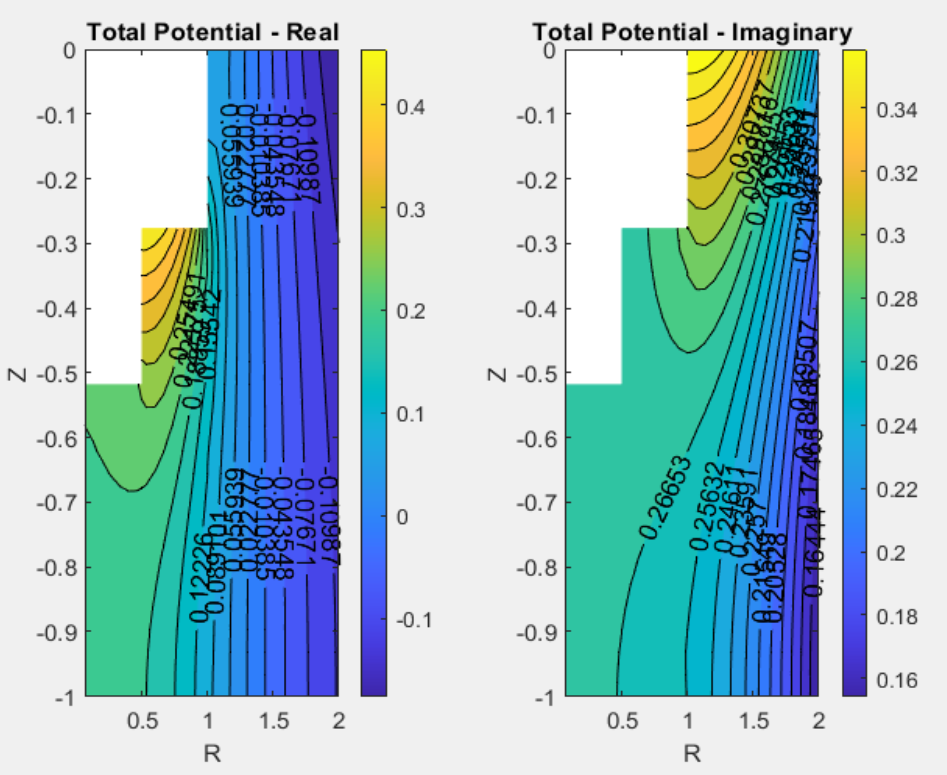
But running doesn't mean working: for some reason, the matching of adjacent fluid zones wasn't being enforced, and one of the boundary conditions that depends on the eigen-coefficients (the radial no-flux condition at the body boundary) was also violated. We debugged for a while, couldn't figure it out, and eventually submitted our class project with our best attempt, noting the discrepancy and saying it is "an area for future work." Here's a figure from that original Dec 2022 version:

You can see the incorrect lack of matching in the abrupt color change at R=1, as well as the unsatisfied boundary condition in the slant of the orange Re(phi)=30 contour (that contour should be horizontal at R=1, to obey the no-flux condition into the body).
We came back in the spring ready to fix the error, hoping our fresh eyes would make debugging quick. And with several hours spent every week, we were able to identify and fix a few small errors over that semester, but we still kept seeing results with incorrect matching. I'm a MATLAB / physical modeling whiz and the partner I was working with coded professionally before his PhD, and all the math had been figured out decades ago. Why was this so hard? Here's why:
The matrix structure of the problem: We knew that the evaluated potential (essentially a weighted sum of our solved 40-element coefficient vector x) was wrong, but since x came from an Ax=b linear solve, it was almost impossible to trace that back to which element(s) in our 40x40 A matrix or 40-element b-vector might be the cause. Even if we knew which elements were the problem, it would still be ambiguous which part of the many-step derivation for the expression needed to be modified.
The papers contained hardly any details about the method's implementation (in the 80s, journal papers were still extremely terse because each page added to print costs, and a more recent 2010 version we were following was a conference paper just 4 pages long). Because of this terseness, and in general the lack of explanations (the papers were probably written with the audience of expert hydrodynamicists, not first and second year grad students), we had to guess at what they meant in a few places.
Only the final numerical results were included in the original paper, not any information about intermediate results. This made debugging way more difficult because of the lack of expected values to compare to. For instance, there was no discussion of the A matrix values, not just numerically but even which elements were real/imaginary and what the sparsity structure should be. We also couldn't compare to other more typical calculation methods (i.e. Boundary element method) because those do not use the A, b, or x matrix/vectors, and compute the potential a different way.
When we contacted Prof. Yeung asking where we might be going wrong, he directed us to a self-published corrected version of the 1980 paper we had never seen before, which in addition to the 3 errors that had been corrected in the official erratum, contained 4 more error corrections not described elsewhere.
The original paper, nor any of the handful of other papers that have used the method in the last several decades, do not publish any code open-source. (We systematically checked every citation). When we inquired, Prof. Yeung said "I won't be able to release our research code to the public. It is not that I don't trust you, experience showed that such a release had often led to multiple versions of our work and some could lead to a chain of questions when the code is modified..."
But Prof. Yeung's email response (May 2023) did point out that our coefficients were real when they should have been complex, which was an important conceptual error. I had an internship that summer, and returned in Fall 2023 to fix that with an improved conceptual understanding of the method. By October, we had finally achieved matching (yay!), but were still having issues satisfying the no-flux condition on the radial body faces.

This time Prof. Yeung didn't reply to our query, and we had read and re-read the papers and our code so many times at this point, that we had nothing left to try but a brute-force debugging approach. Two details in the paper that were never clarified in the derivation were which bounds to integrate over and which eigenfunction to multiply by for orthogonality. So in January 2024 I made the following figure, trying out every combination:

No combination satisfied both the matching condition and the radial no-flux condition, but the exercise did give us a more nuanced understanding of which bounds and multiplication should have been correct and why. We also hired an MEng student that spring to start porting the MATLAB code over to python, and by writing down our equations clearly for him to implement, we mastered the final conceptual nuance that hadn't been explained in the original paper: the effect on the matrix structure of using a different number of terms in each fluid region.
By this time it was February 2024, and we were 100% conceptually sound on every detail of the implementation, but still unable to get results with both matching and the no-radial-flux boundary condition. We slogged on, systematically checking and double checking, still nothing.

Finally in late April and early May, in what felt like a miracle, I caught two typos: a misplaced parenthesis, and a missing period (a conjugate transpose that should have been just a transpose).

I had done it!
Here's the first potential plot that satisfied all boundary and matching conditions:
In honor of the name of the method (MEEM), I also made a meme, which I shared at lab meeting along with a description of the method and the technical and nontechnical lessons learned from our efforts over the last year and a half.

Stepping back, what had we just accomplished? It had taken two competent PhD students 1.5 years (a little over a year, if you subtract the summer) of continuous work for several hours a week to replicate a single decades-old paper, in consultation with the paper's original author and a variety of external resources.

This might be understandable for experimental work, large multi-disciplinary analyses, or anything involving randomness or data, but it is outrageous for a purely mathematical/computational paper where it took less than two weeks to do the basic implementation and the final product is only a few hundred lines of code .
My lab already was in the good habit of publishing all our code open source, but this experience made me a much stronger advocate for open-source and replicable research, and also for simply including sufficient information in the paper to explain the work to non-experts. With proper documentation, there is no reason that should have to take anyone else as long as it took us.
I presented our re-implementation of the method at the University Marine Energy Research Community (UMERC) conference that summer, documenting the answers to all the conceptual and implementation questions that the prior papers left ambiguous, in a way that typical engineers could understand. Our paper is available here: https://doi.org/10.5281/zenodo.15168251.
My presentation received the "Award for the best communication of complex mathematics," which was not previously and has not since been an award category at this conference, so I suspect they made it up specifically for me. While I'm proud to have communicated so effectively, I wish that this weren't as rare as it is in academia, and that computationally effective methods are democratized and documented for all to use.
Since then, I've worked with a fantastic team of undergrads and MEng students to release an open-source python package for the method. It features an object-oriented structure designed to be future-proof for extensions to other geometries, and outputs results in a format compatible with Capytaine, the typical numerical open-source hydrodynamics solver that the method is designed to replace. It also has a snazzy GUI, tutorial, and documentation site. We've submitted to the Journal of Open Source Software and are working on a paper with numerical details for the Journal of Fluid Mechanics. Package available here (OpenFLASH): https://zenodo.org/records/17695396




Comments